cissoid

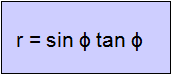
The cissoid ¹⁾ can be constructed as follows:
Given a circle C with diameter OA and a tangent l through A. Now, draw lines m through O, cutting circle C in point Q, line l in point R. Then the cissoid is the set of points P for which OP = QR.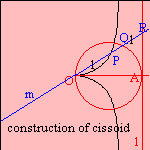

This construction has been done by the Greek scholar Diocles (about 160 BC) ²⁾. He used the cissoid to solve the Delian problem, dealing with the duplication of the cube. He did not use the name cissoid. The name of the curve, meaning 'ivy-shaped', is found for the first time in the writings of the Greek Geminus (about 50 BC). Because of Diocles' previous work on the curve his name has been added: cissoid of Diocles.
Roberval and Fermat constructed the tangent of the cissoid (1634): from a given point there are either one ore three tangents.
In 1658 Huygens and Wallis showed that the area between the curve and his asymptote is π/4.

The cissoid of Diocles is a special case of the generalized cissoid, where line l and circle C have been substituted by arbitrary curves C1 and C2.
The curve, having one cusp and one asymptote, has as Cartesian coordinates: x³ + xy² - y² = 0 or y² = x³/(1-x)

Another generalization of the curve is the ophiuride. 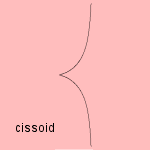Some relationships with other curves are:

• the curve is a pedal as well as the polar inverse (with the cusp as center of inversion) of the parabola
• its catacaustic (with the cusp as source) is the cardioid
• when a parabola is rolling over another (equal) parabola, then the path of the vertex is a cissoid
• its pedal (with the focus as pedal point) is the cardioid

In the special case that construction line l passes through the center of the circle, the curve is a strophoid.
And near the cusp the curve approaches the form of a semicubic parabola.

notes

1) In Italian: cissoide di Diocle.

2) Waerden 1950 p.297