|

where 0 < b < π/2.
When the constant a is rational, the curve is algebraic and
closed.
If a is irrational, the curve fills the area [-1,1] x [-1,1].
It is easy to see that the curves for 1/a and a are equal in form. This means that we can
confine ourselves to the case a < 1.
Jules-Antoine Lissajous (1822-1880) discovered these elegant curves (in 1857) while doing
his sound experiments.
But it is said that the American Nathaniel Bowditch (1773-1838)
found the curves already in 1815. After him the curve bears the name of
Bowditch curve.
Another name that I found is the play curve of Alice1.
The curves are constructed as a combination of two perpendicular harmonic
oscillations. Patterns occur as a result of differences in frequency ratio (a) and phase (b).
At high school we used the oscilloscope to make the curve visible (nowadays a computer
would do), by connecting different harmonic signals to the x- and y-axis
entrance. The curves have applications in physics, astronomy and other sciences.
Each Lissajous curve can be described with an algebraic equation.
Write a as the smallest integers m, n for which a = m/n. Then the degree of the equation obeys the following rules:
- degree = m
for b = 0 and m is odd
for b = π/2 and m is even
- degree = 2m
for b ∈ ]0,π/2] and m is odd
for b ∈ [0,π/2[ and m is even
Some examples of Lissajous curves are the following:
| a |
b |
name of the curve |
| 1 |
0 |
straight line |
| 1 |
π/2 |
circle |
| 1 |
<> 0, π/2 |
ellipse |
| 2 |
π/2 |
parabola
|
| 2 |
<> π/2 |
besace: its
parameter a is equal to the tangent of the Lissajous curve's parameter b. |
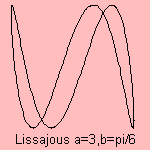
| 3 |
0 |
the cubic y = 2x3 - x (see the picture below) |
| 3 |
π/2 |
the sextic y2
= (1 - x2)(1-4x2)2 (see the picture below) |




In the situation that the parameter a is an integer, three forms of the curve can be distinguished:
- the curve is symmetric with respect to the x- and y-axis
When a is even: b = 0. When a is odd: b = π/2.
- the curve is asymmetric
For this form (and the one before, as a matter of fact) the number of compartments is
equal to the value of a.
- the curve has no compartments, the two parts of the curve come
together
When a is even:
b = π/2. When a is odd: b = 0.
There is a relation with the Tchebyscheff
polynomial: the Lissajous curve (a, b) corresponds with Tchebyscheff
function Ta for a integer and b=π/2 (for even a) or b=0 (for odd a).
The Lissajous curve can be extended to the
notes
1) In French: joue courbe d'Alice.
|












