more circles

conic section
 

This page is dedicated to curves that are made from more than one circle.

In Venn diagrams each collection is represented by a circle, as a visual help to derive rules for the intersections.

A polygon build of circle arcs is called a curvilinear polygon.
An example with two arcs is the lens.

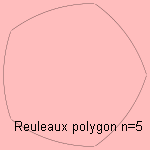A Reuleaux polygon is a curvilinear polygon where the center of each circle arc is the opposite point of the polygon.
Each Reuleaux polygon is a curve with constant width.
Most known example is the three arc Reuleaux triangle, a curvilinear triangle.

Two circles
Two circles we find in the English bicycle1), and the French bicyclette.

By two (equal) arcs a lens or lemon curve can be formed. This is a curvilinear polygon.
This is an old symbol, denoting a fish as well as the female vulva.
For Pythagoras it was the symbol of the intersection of the world of the divine (one circle) with the world of matter (other circle).
Later the sign was adopted by the Christians, with names as:

Extending the arcs in one side results in the Christian ichtus symbol.
An annulus is the form of two concentric circles, the shape of a ring.









A more recent use is a pattern formed in the shape of two circle arcs, the stamp of Truchet. The pattern consists of two different orientations of the stamp next to each other, in an arbitrary sequence orientation.
These patterns have been used in the construction of games, e.g. the 'black path game' and 'meander'.
The pattern was found by Cyril Stanley Smith, who wrote an article 2) about Truchet. Smith was a metallurgist and historian of technology at MIT who studied crystals.
The pattern described by Truchet was the Truchet tiling.

Three circles
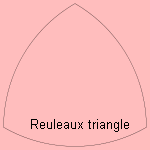 A circular triangle is formed by three (equal) arcs.
In the case of three equal arcs beginning in the angles of an equal triangle, it is called the Reuleaux triangle. This triangle can be rotated inside a square, so making it possible to drill a hole with (nearly) the shape of a square.

 

 

Archimedes described the arbelos or shoemaker's knife. The curve resembles the blade of a knife used by ancient cobblers. 
It appears that the arbelos has some remarkable qualities, for instance:

  1. the arc length along the enclosing semicircle is the same as along the two smaller semicircles
  2. draw a perpendicular from the tangent of the two semicircles to the edge of the large circle. Then the area of the circle with as diameter the perpendicular is the same as the area of the arbelos

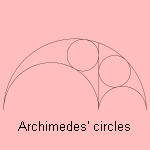The two circles inscribed on each half of the perpendicular are called the Archimedes' circles or the twin circles of Archimedes. Circles in the arbelos that are congruent (i.e. equal radius) to these circles are called Archimedean circles.

Now, let's denote the left semicircle as C, with center (-c, 0) and the right semicircle as D, with center (d,0). C and D touch at O, E is the large semicircle.
Now define semicircles C(nc) and D(nd), with centers (-nc,0), (nd,0) respectively, which touch in O. Then Schoch's circle S is the circle that touches E internally and C(2c) and D(2d) externally.
Woo considered the Schoch line w through the center of the Schoch's circle and parallel to the y-axis.
Now it appears that the circles with center on the Schoch line and touching C(nc) and D(nd) externally are also Archimedean circles, and they are called Woo circles.

Thomas Schoch and Peter Woo studied these circles, H. Okumura and M. Watanabe made a generalization of the circles.

 

 

 

 

The Pappus chain is made by constructing tangent Pappus circles in the arbelos, from right to left in the picture. The centers of the circles lie on an ellipse.
The Bankoff circle B is the circle through the cusp of the arbelos and the tangent points of the first Pappus circle.
Leon Bankoff (1908-1997) was an American dentist and mathematician. He became a prominent Los Angeles dentist with famous patients of the Beverly Hills-Hollywood scene.

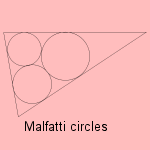Given a triangle, put three circles in it, so that each circle is tangent to the other two and to two sides of the triangle. These circles are the Malfatti circles.
These were for many years considered to provide a solutions for the so-called Malfatti´s problem, later it appeared they are not.
Giovanni Francesco Malfatti (1731-1807) was an Italian mathematician in Ferrara.

Four circles
Archimedes constructed the salinon as a combination of four semicircles. The centers of the circles are lying on a line, the two small circles are of equal size. Archimedes described the curve, that is also called the salt-cellar 4), in his Book of Lemmas.

More concentric circles can be found at a target for shooting or darting.
In the 16th century scientists as Giordano Bruno and John Dee looked at the spiritual meaning of so-called hermetic forms, which often contained circles. By placing those circles in the right place a resonance with his celestial (pure) counterpart could be reached. An example of these forms is - with four circle arcs - John Dee's magic hieroglyphic 5).

 

 

 

 

 

 


 

 

The circle skating rink curve is formed by four circle arcs, one four each side, so that the curve is tangent to two concentric circles (of different size).
The four arcs are from circles with the same size, but different center.

The curve is a simplification of the Saint-Hilaire skating rink curve. The physicist Saint-Hilaire was the first to calculate the profile of this curve.

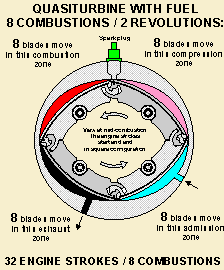An application of the profile has been found in engine design. The Quasiturbine (or Qurbine) is a rotating engine with a rotor, trapped inside an internal housing contour, which does not require a central shaft or support. This concept brings the engine dead time to zero.
The method of operation allows the engine to be extremely flexible. The developer claims that it is possible to use it for pneumatics, hydraulics, steam, petrol, natural gas and hydrogen.

The precise formula is not yet available to me, it can be found in the patent for this engine.

Five circles
A combination of five circles we can see in the symbol of the car Audi - circles placed on one line - and in the symbol of the Olympic games - the five continents, the circles now positioned in two lines. Is this similarity the explanation for the sponsorship of Audi of the Dutch Olympic team?
A circle placed around a cross is the symbol of the Ku-klux klan 6) movement.

Infinite circles
An infinite sequence of tangent circles for which the radius converges to zero, is called a Hawaiian earring.
The radius can have forms like 1/n (see picture) or 1/n2 (n=1,2, ...).
The topology of this set and its generalizations has been studied by Eda and Kawamura.

 


notes

1) Bi (Gr.) = two.

2) He wrote in the journal Leonardo, The Tiling Patterns of Sebastien Truchet and the Topology of Structural Hierarchy, Leonardo 20, pp 373-385 1987.

3) Memoir sur les Combinasions

4) Two explations of the word 'salinon' can be found:

  • the word 'salinon' resembles the Greek word for a vessel for water, what is the form of the curve, turned upside down
  • the word salinon is a graecised form of the Latin word salinum, what is a salt-cellar. The lower curve resembles an ordinary type of salt-cellar.

5) Davis 1981 p. 100.

6) Ku-klux is derived from the Greek word for circle: kyklos.