logarithmic prime counting approximation

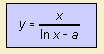
The function approximates the prime counting function.

The first order approximation (a=0) follows from the Prime Number Theorem, which has been suggested by Friedrich Gauss.

In 1808 Legendre found that for a = 1.08366 the formula gives an even better approximation for the prime counting.

In 2003 Roberto Neumann found a variant on this function that approximates the prime counting even better, with the Neumann prime counting approximation:

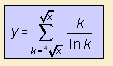
where the values of the square roots are rounded before using them in the summation.

A comparison of these approximations can be found at www.c-eagle.com.