besace

The besace is a Lissajous curve. In 1750 Cramer gave the curve its name ¹⁾.

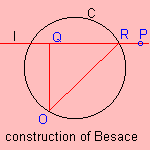
The curve can be constructed as follows: given a circle C and a point O draw horizontal lines l which cut the circle in R. Q is the projection of O on l. Then the Besace is the set of points P for which PQ = OR.

The curve is the result of the projection of the pancake curve on a plane through the central z-axis of the curve.

For large a, the curve approximates the parabola.

For a = 0 the lemniscate of Gerono results:

The form of the curve is that of ribbon ²⁾, as the other lemniscate, the more famous lemniscate of Bernoulli. Because of the resemblance with the digit 8, the curve is also called the (figure) eight curve.
But I think the figure eight curve that is formed by the hippopede makes a better eight.

Its Cartesian equation resembles the equation of the kampyle of Eudoxus.

notes

1) In German: Quersackkurve.

2) lemniskos (Gr.) = ribbon