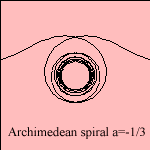
Archimedean spiral

This spiral is a generalization of Archimedes' spiral (a=1), named to the Greek Archimedes (225 BC).
The inverse of the spiral with a constant a is an Archimedean spiral with a constant -a.


There are some special situations:

• a = -1: hyperbolic spiral
• a = -1/2: lituus
• a = 1/2: Fermat's spiral
• a = 1: Archimedes' spiral

An Archimedean spiral with parameter a has as polar inverse an Archimedean spiral with parameter -a: so the lituus and Fermat's spiral are inversely related, and also the hyperbolic and the Archimedes' spiral.

It was Sacchi (1854) who distinguished this group of spirals, for the first time.