
|
 |
 |
 |
 |
 |
 |
curvature curve |
main |
There are four derived curves that are related to curvature:
Given a curve C1, the evolute
is the curve C2 defined by the loci of the centers of curvature of C1. In other
words:
construct in each point P of curve C1 a circle that is a tangent to C1 in P; then the
center of the circle belongs to C2.
When C1 is given by (x, y) = (f(t), g(t)), then C2 has the form:
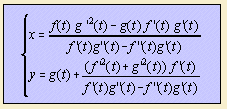
If a line l rolls without slipping as a tangent along a curve C1,
then the path of a point P on l forms a new curve C2, the involute
of C1. Involution is the reverse operation of evolution: if C2 is the involute of
C1, then C1 is the evolute of C2.
You might ask yourself whether there exists a curve whose involute is exactly the same
curve. Well, there are two curves with this property:
Besides, there are some curves whose involute is the same curve, but not equal in position or magnitude:
Some other involute-evolute couples are:
| involute | evolute |
| ellipse | astroid |
| epicycloid | epicycloid (similar, but smaller) |
| involute of a circle | circle |
| orthotomic | caustic |
| tractrix | catenary |
| roulette: when a line is rolling over curve C, the path of any point on the line. | any curve C |
In fact, the evolute of a curve is the same as the envelope of its normal.
The radial is a variation on the evolute: draw, from a fixed point, lines parallel to the radii of curvature, with the same length as the radii. The set of end points is the radial. The logarithmic spiral is the curve whose radial is the curve itself.
Radials of some other curves are:
| base curve | radial |
| astroid | quadrifolium |
| catenary | kampyle of Eudoxus |
| Cayley's sextic | nephroid |
| cycloid | circle |
| deltoid | trifolium |
| epicycloid | rhodonea |
| parabola | semi cubical parabola |
| tractrix | kappa curve |
Given a curve, the curvature κ is defined as the inclination per arc length:
κ(s) = dφ/ds.
This curvature can be expressed for a curve y = f (x) as follows:
![]()
If the
curvature is positive (>= 0), we speak of a convex
curve.
If the curvature is strictly positive (>0), we speak of a strictly
convex curve.
If the curvature is negative (<= 0), we speak of a concave
curve.
If the curvature is strictly negative (<0), we speak of a strictly
concave curve.
Given the curvature as function of the arc length, you can look for the
representing curve.
Some example curves are the following:
| κ = dφ/ds | curve |
| 1 | circle |
| 1 / s | logarithmic spiral |
| 1 / √s | involute of a circle |
| s | Euler´s spiral |
| s2 | double clothoid |
| ∑ai si | polynomial spiral |
| a sin s | meander curve |
The radius of curvature R is the reciprocal of the absolute value of the curvature κ, so that R = 1/κ.
The Cesaró equation writes a curve in terms of a radius of curvature R and an arc length s.